Plasma edge simulations

Transport simulations in the edge region of tokamak plasmas with an high-order HDG scheme: the MHDG code

The MHDG code is a suite of Fortran routines developed to simulate the transport of mass, momentum and heat in the edge region of tokamak plasmas, in 2D and 3D geometries. It uses a high-order HDG scheme to discretize the plasma fluid equations. In MHDG, the tokamak geometry is discretized using high-order unstructured meshes of curved triangles and quadrilaterals for the poloidal plane and a structured discretization in the toroidal direction. The computational mesh is completely non-aligned with the magnetic field lines. MHDG takes advantage of MPI/OpenMP parallelization techniques, and links to optimized libraries for linear algebra, using either parallel direct linear solvers (PaStiX), either preconditioned iterative solvers based on Krylov methods and multi-grids schemes.

Thanks to the non-alignement of the computational mesh, equilibrium-evolving simulations are possible with MHDG. Below is the simulation of a discharge in the tokamak WEST using magnetic configurations reconstucted from the experiments (simulation performed by Manuel Scotto).

Using simulated equilibrium transitions, for example with the code CEDRES++, it is also possible to study the response of the plasma at different transition speed. Below is the simulation of the transition from the limiter configuration to the divertor one, and the response of the plasma to two different transition speeds.

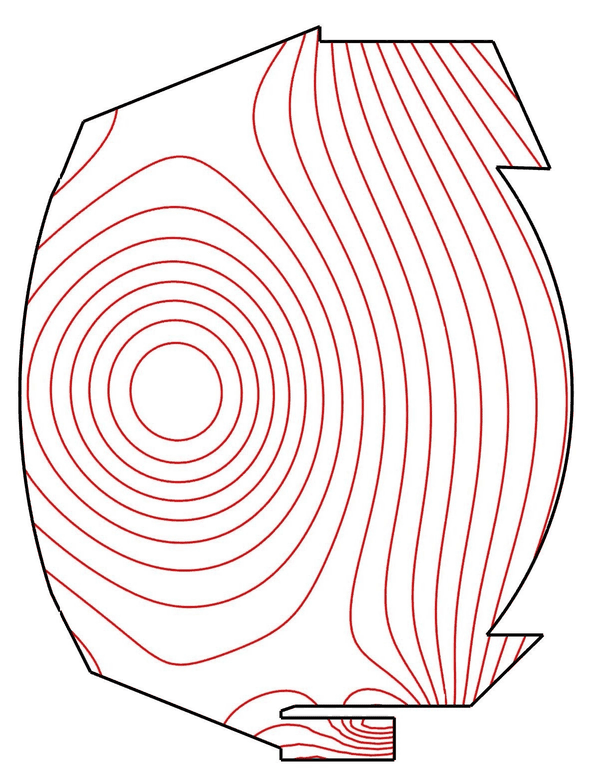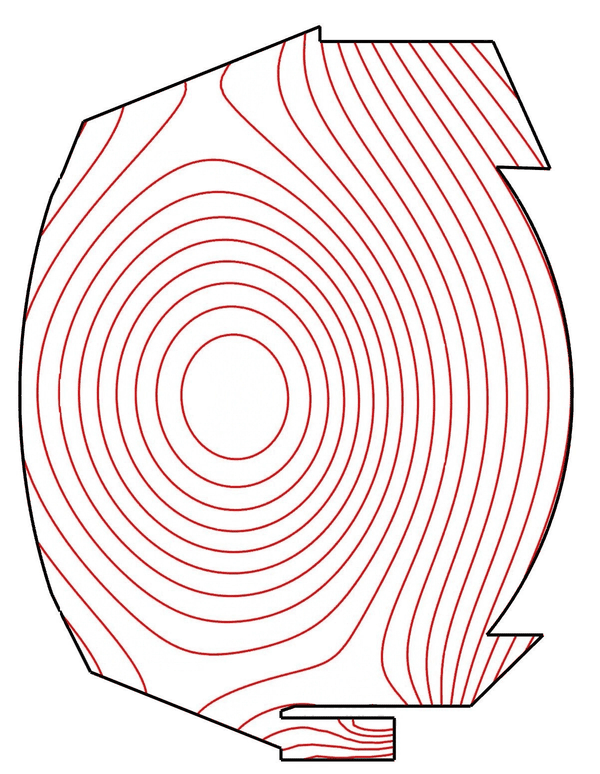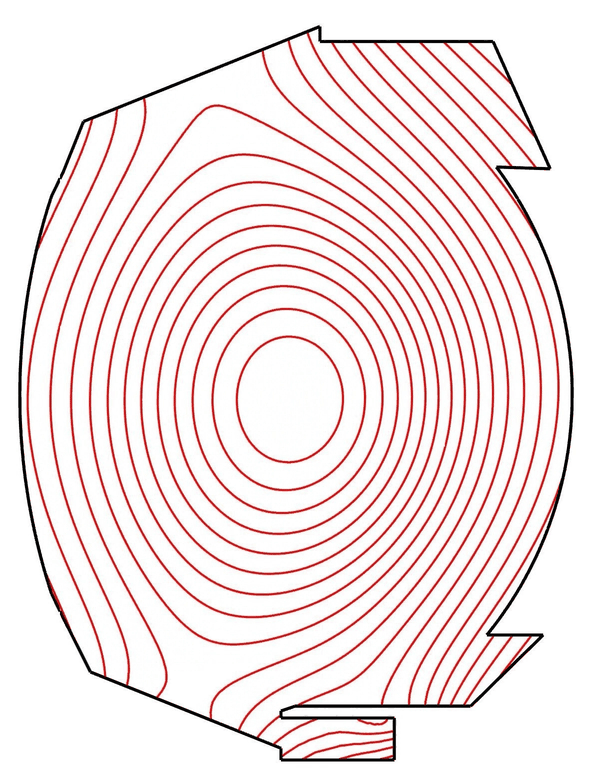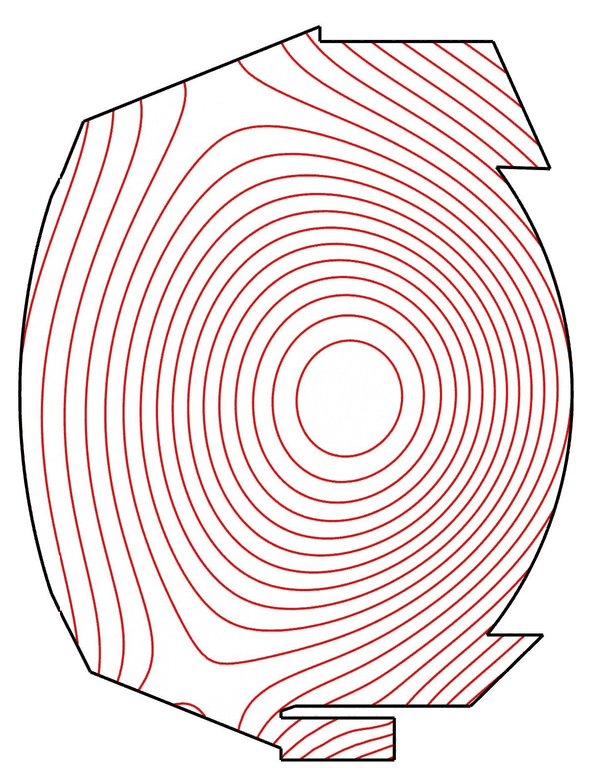
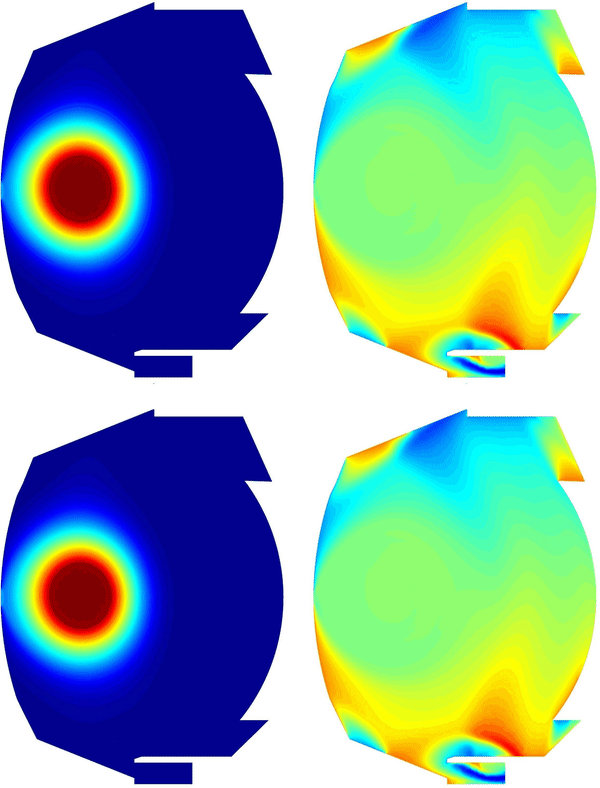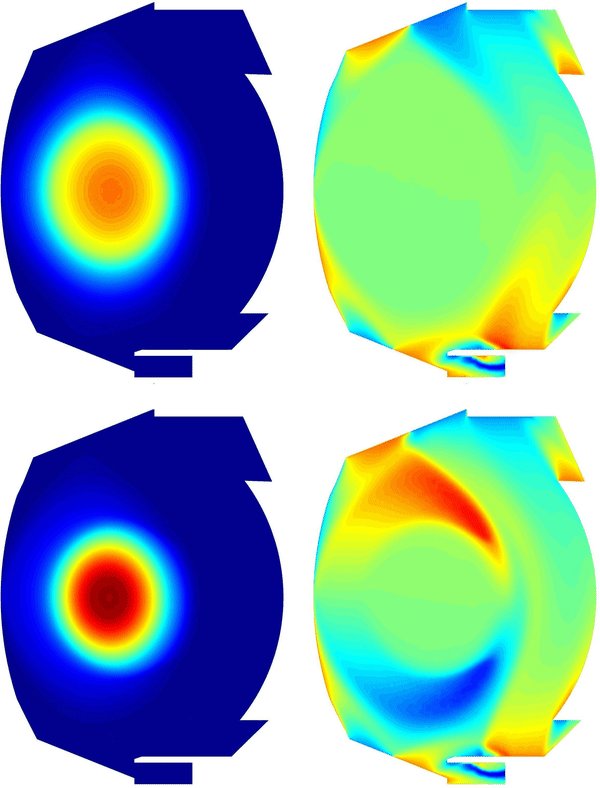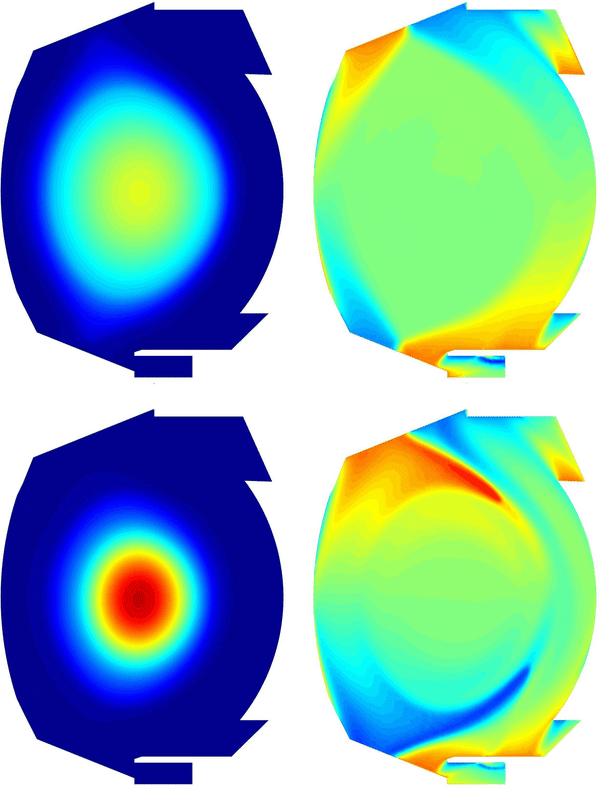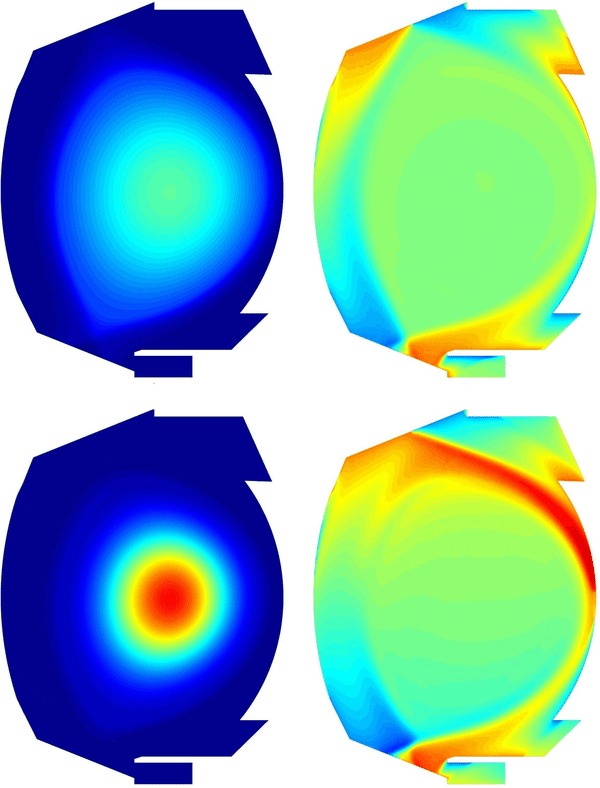
MHD simulations of Kelvin-Helmholtz instabilities in tokamak plasmas

In the scrape-off layer (SOL) of tokamaks, the flow acceleration due to the presence of limiter or divertor plates rises the plasma velocity to a sonic regime. These high velocities imply the presence of a strong shear between the SOL and the core of the plasma that can possibly trigger some parallel Kelvin-Helmholtz instabilities. Using a 3D finite volume scheme, a numerical study of the edge plasma is carried out. This method combines the use of triangular unstructured meshes in the poloidal section and structured meshes in the toroidal direction and it is particularly suited to the representation of the real complex geometry of the vacuum chamber of a tokamak. The numerical results confirm that in agreement with the theoretical expectations as well as with other numerical methods, the sheared flows in the SOL are subject to parallel Kelvin-Helmholtz instabilities. However, the growth rate of these instabilities is low and these computations require both a sufficient spatial resolution and a long simulation time. This makes the simulation of parallel Kelvin-Helmholtz instabilities a demanding benchmark.

New: the ANR SISTEM