Giorgio Giorgiani
Applied Mathematician at ITER
Tel: +33 (0)6 95 39 38 17

Finite-element computations with Powell-Sabin splines
Powell-Sabin splines are piecewise quadratic polynomials with a global C1 continuity, defined on conforming triangulations. I am interested in exploring the performances of this kind of splines when used as shape functions in a finite-element method. The global smoothness of the C1 space has a beneficial stabilization effect in the treatment of advection-dominated equations and leads to a better capturing of thin layers. Moreover, unlike most of other typology of high-order finite elements, the numerical unknowns in PS elements are located in the vertices of the triangulation, leading to an easy treatment of the parallel aspects.
Key issues:
-
Definition of the Powell-Sabin refinement.
-
Determination of the control triangles for each vertex: the control triangle is chosen as the minimal area triangle enclosing the control points (right figure). This guarantees optimal shape functions from a numerical point of view.
-
For the imposition of the boundary conditions, the control triangle must be aligned with the boundary (two figures below).



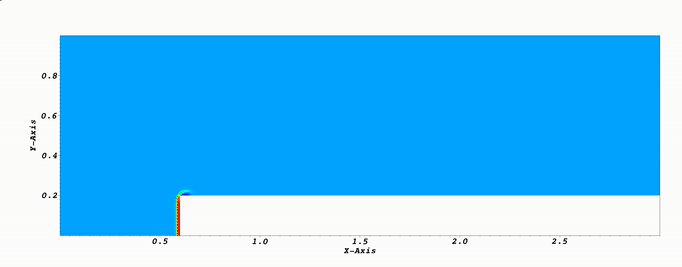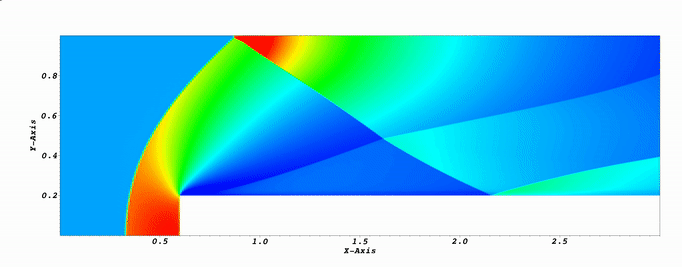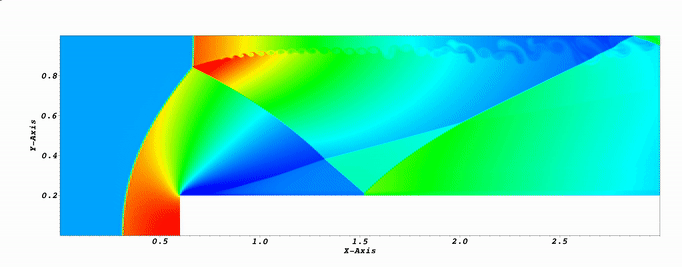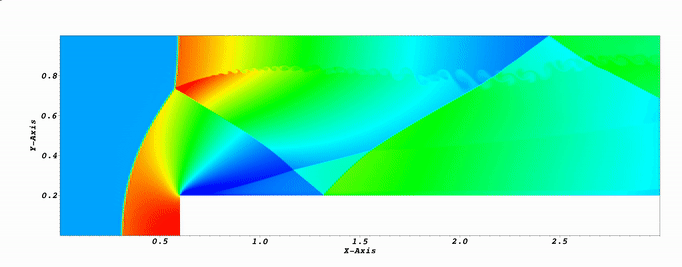
Application: solution of the 2D inviscid Euler equations in supersonic regime. I used a stabilized formulation, with a SUPG and shock capturing term. The numerical examples presented below are 1) the forward facing step at M=3 and 2) the Double Mach reflection test at M=10.